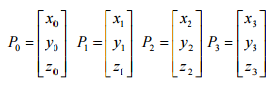#include<iostream.h>
#include<graphics.h>
#include<conio.h>
#include<stdlib.h>
void main()
{
int gr_driver = DETECT,gr_mode;
initgraph(&gr_driver,&gr_mode,"../bgi");
setcolor(1);
arc(250,250,0,180,50);
setcolor(2);
arc(240,240,0,180,50);
setcolor(3);
arc(230,230,0,180,50);
setcolor(4);
arc(220,220,0,180,50);
setcolor(5);
arc(210,210,0,180,50);
setcolor(6);
arc(200,200,0,180,50);
setcolor(7);
arc(260,260,0,180,50);
setcolor(8);
arc(270,270,0,180,50);
setcolor(9);
arc(280,280,0,180,50);
setcolor(10);
arc(290,290,0,180,50);
//
setcolor(1);
arc(350,250,180,0,50);
setcolor(2);
arc(340,240,180,0,50);
setcolor(3);
arc(330,230,180,0,50);
setcolor(4);
arc(320,220,180,0,50);
setcolor(5);
arc(310,210,180,0,50);
setcolor(6);
arc(300,200,180,0,50);
setcolor(7);
arc(360,260,180,0,50);
setcolor(8);
arc(370,270,180,0,50);
setcolor(9);
arc(380,280,180,0,50);
setcolor(10);
arc(390,290,180,0,50);
line(150,200,240,290);
line(350,200,440,290);
getch();
closegraph();
}CNTT-ĐHThành Đô
Kĩ Thuật Đồ họa (Đường cong, mặt cong 3D)
Lưu Văn Bình 1300783 || Trần Văn Hòa || Phan Thị Quỳnh Mai || Nguyễn Văn Hiển || Nguyễn Thị Giang || Bùi Thanh Lam
Chủ Nhật, 6 tháng 9, 2015
Mặt cong B-Spline
1. Mặt cong B-Spline
Phương trình mặt B-spline:
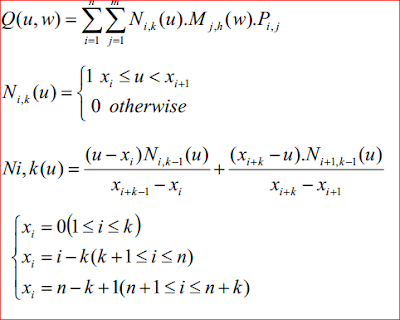
P
ij là điểm kiểm soát
N và M là đa thức B-spline
Với các mặt cong mở mặt cong phụ thuộc vào các nút vector
Đặc điểm của mặt cong B-Spline
*ƒ Số bậc caonhất của bề mặt theo mỗi hướng thì bằng số điểm kiểm soát -1 theo hướng đó.
ƒ *Đạo hàm riêng của phương trình bề mặt theo mỗi tham biến có bậc bằng số điểm kiểm
soát theo tham biến đó trừ 2.
ƒ* Bề mặt B-spline thì không chịu ảnh hưởng của phép biến đổi anfine. Bề mặt sẽ thay đổi
nếu ta thay đổi đa giác kiểm soát.
ƒ *Ảnh hưởng của một điểm kiểm soát đơn được giới hạn bởi + - k/2 h/2 khoảng đối với mỗi
tham số.
ƒ *Nếu số đỉnh của đa giác kiểm soát bằng số bậc theo mỗi tham biến và không có điểm kép
nào thì mặt B-spline sẽ chuyển thành mặt Bezier.
ƒ* Nếu các đa giác kiểm soát có dạng tam giác thì lưới đa giác kiểm soát sẽ có hình dáng gần
giống với bề mặt cong.
ƒ* Mỗi mặt B-Spline luôn nằm trong bao lồi của đa giác kiểm soát .
ƒ* Mỗi mặt B-Spline có dáng điệu luôn bám theo hình dáng của đa giác kiểm soát.
Phương trình mặt B-spline:
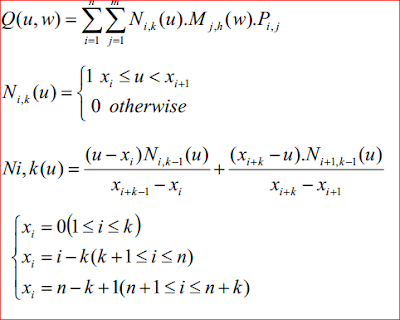
P
ij là điểm kiểm soát
N và M là đa thức B-spline
Với các mặt cong mở mặt cong phụ thuộc vào các nút vector
Đặc điểm của mặt cong B-Spline
*ƒ Số bậc caonhất của bề mặt theo mỗi hướng thì bằng số điểm kiểm soát -1 theo hướng đó.
ƒ *Đạo hàm riêng của phương trình bề mặt theo mỗi tham biến có bậc bằng số điểm kiểm
soát theo tham biến đó trừ 2.
ƒ* Bề mặt B-spline thì không chịu ảnh hưởng của phép biến đổi anfine. Bề mặt sẽ thay đổi
nếu ta thay đổi đa giác kiểm soát.
ƒ *Ảnh hưởng của một điểm kiểm soát đơn được giới hạn bởi + - k/2 h/2 khoảng đối với mỗi
tham số.
ƒ *Nếu số đỉnh của đa giác kiểm soát bằng số bậc theo mỗi tham biến và không có điểm kép
nào thì mặt B-spline sẽ chuyển thành mặt Bezier.
ƒ* Nếu các đa giác kiểm soát có dạng tam giác thì lưới đa giác kiểm soát sẽ có hình dáng gần
giống với bề mặt cong.
ƒ* Mỗi mặt B-Spline luôn nằm trong bao lồi của đa giác kiểm soát .
ƒ* Mỗi mặt B-Spline có dáng điệu luôn bám theo hình dáng của đa giác kiểm soát.
Tóm tắt:
Việc tạo ra các đường cong theo ý muốn cũng là vấn đề thường gặp khi làm việc với đồ hoạ
máy tính. Chúng ta khảo sát cách tiếp cận vẽ đường cong bằng Hermite, Bezier và B-spline. Các
cách tiếp cận này dựa trên cơ sở vẽ đường cong bằng một tập điểm mô tả hình dáng của đường
cong gọi là tập điểm kiểm soát. Khi thay đổi tập điểm này, hình dáng của đường cong sẽ thay đổi
theo. Cách tiếp cận này cho thấy sự thuận lợi và linh hoạt khi cần phải vẽ các đường cong phức
tạp và do đó nó được dùng nhiều trong thiết kế.
Một nhược điểm trong cách vẽ đường cong bằng Bezier là khi một phần của đường cong đã
đạt yêu cầu, nhưng khi hiệu chỉnh phần còn lại sẽ mất đi phần đã đạt yêu cầu, hay việc nối trơncác đường cong sẵn có. Để khắc phục các vấn đề này ta có cách tiếp cận cải tiến vẽ đường cong
bằng B-spline.
Tương tự như vậy việc biểu diễn các mặt cong trong đồ hoạ máy tính cũng là một vấn đề
cần thiết để mô tả đối tượng trong thế giới thực. Chúng ta khảo sát về các phương pháp biểu diễn
mặt cong thông qua phương trình tham số. Trong đó, phương trình tham số của một mặt có dạng
là một phương trình tham số hai biến p(u,v) và một điểm bất kỳ trên mặt sẽ được biểu diễn dưới
dạng p(u,v)= (x(u,v), y(u,v), z(u,v)). Chúng ta khảo sát một số mặt đơn giản như: mặt kẻ, mặt tròn
xoay, mặt trượt và mặt Boolean Sum.
Trên cơ sở các đường cong bằng Hermite, Bezier và B-spline chúng ta cũng xây dựng được
các mặt Hermite, Bezier và B-spline.
Việc tạo ra các đường cong theo ý muốn cũng là vấn đề thường gặp khi làm việc với đồ hoạ
máy tính. Chúng ta khảo sát cách tiếp cận vẽ đường cong bằng Hermite, Bezier và B-spline. Các
cách tiếp cận này dựa trên cơ sở vẽ đường cong bằng một tập điểm mô tả hình dáng của đường
cong gọi là tập điểm kiểm soát. Khi thay đổi tập điểm này, hình dáng của đường cong sẽ thay đổi
theo. Cách tiếp cận này cho thấy sự thuận lợi và linh hoạt khi cần phải vẽ các đường cong phức
tạp và do đó nó được dùng nhiều trong thiết kế.
Một nhược điểm trong cách vẽ đường cong bằng Bezier là khi một phần của đường cong đã
đạt yêu cầu, nhưng khi hiệu chỉnh phần còn lại sẽ mất đi phần đã đạt yêu cầu, hay việc nối trơncác đường cong sẵn có. Để khắc phục các vấn đề này ta có cách tiếp cận cải tiến vẽ đường cong
bằng B-spline.
Tương tự như vậy việc biểu diễn các mặt cong trong đồ hoạ máy tính cũng là một vấn đề
cần thiết để mô tả đối tượng trong thế giới thực. Chúng ta khảo sát về các phương pháp biểu diễn
mặt cong thông qua phương trình tham số. Trong đó, phương trình tham số của một mặt có dạng
là một phương trình tham số hai biến p(u,v) và một điểm bất kỳ trên mặt sẽ được biểu diễn dưới
dạng p(u,v)= (x(u,v), y(u,v), z(u,v)). Chúng ta khảo sát một số mặt đơn giản như: mặt kẻ, mặt tròn
xoay, mặt trượt và mặt Boolean Sum.
Trên cơ sở các đường cong bằng Hermite, Bezier và B-spline chúng ta cũng xây dựng được
các mặt Hermite, Bezier và B-spline.
Mặt cong Bezier
2. Mặt cong Bezier
Mảnh-patch Bézier:
Hình vẽ: Mặt cong Bezie
= a3(v)
Mảnh-patch Bézier:
Hình vẽ: Mặt cong Bezie
= v P01 + (1 - v)P00 + a3(v) -(1 - v)P00 - v P01
= a3(v)
Mặt cong bậc ba Hermit
3.Mặt cong bậc ba Hermit:
Phải đảm bảo là đường cong không gian với 3 trục toạ độ x, y, z. Tránh được những tính toán phức tạp và những phần nhấp nhô ngoài ý muốn xuất hiện ở những đường đa thức bậc cao. Công thức mô tả:
Tường minh : y = f3 (x),z = g3 (x)
Không tường minh: f3 (x,y,z) = 0
Biểu diễn các đường cong tham biến (Parametric representation):
x = f3 (u), y = f3 (u), z = f3 (u) trong đó u ∈[0 1]
Theo Lagrange:
x = a1 + b1u + c1u2 + d1u3 y = a2 + b2u + c2u2 + d2u3 z = a3 + b3u + c3u2 + d3u3
Ở đây ba phương trình với 12 ẩn số
Với 4 điểm p0, p1, p2, p3 phương trình xác định (vì 4 điểm thì xác định 1 đường cong trong không gian).
Mỗi 1 điểm cho ta cặp 3 giá trị:
Cả thảy có 12 phương trình, thay vào 3 phương trình trên ta tính được 12 ẩn a1.....d3
Ghi chú: rõ ràng có sự thay đổi một chút về đường cong thì ta lại phải giải lại hệ phương trình để tính các tham số cho đường cong, dẫn đến tính toán chậm.
Phải đảm bảo là đường cong không gian với 3 trục toạ độ x, y, z. Tránh được những tính toán phức tạp và những phần nhấp nhô ngoài ý muốn xuất hiện ở những đường đa thức bậc cao. Công thức mô tả:
Tường minh : y = f3 (x),z = g3 (x)
Không tường minh: f3 (x,y,z) = 0
 |
| Đường cong đa thức bậc 3 |
x = f3 (u), y = f3 (u), z = f3 (u) trong đó u ∈[0 1]
Theo Lagrange:
x = a1 + b1u + c1u2 + d1u3 y = a2 + b2u + c2u2 + d2u3 z = a3 + b3u + c3u2 + d3u3
Ở đây ba phương trình với 12 ẩn số
Với 4 điểm p0, p1, p2, p3 phương trình xác định (vì 4 điểm thì xác định 1 đường cong trong không gian).
Mỗi 1 điểm cho ta cặp 3 giá trị:
Cả thảy có 12 phương trình, thay vào 3 phương trình trên ta tính được 12 ẩn a1.....d3
Ghi chú: rõ ràng có sự thay đổi một chút về đường cong thì ta lại phải giải lại hệ phương trình để tính các tham số cho đường cong, dẫn đến tính toán chậm.
Mặt nội suy trên bốn đường biên(Boolean sum surface)
4. Mặt nội suy trên bốn đường biên(Boolean sum surface)
Mặt được xây dựng trên 4 điểm và các đường cong biên, S(u,v) mặt nội suy trên 4 đường
biên.
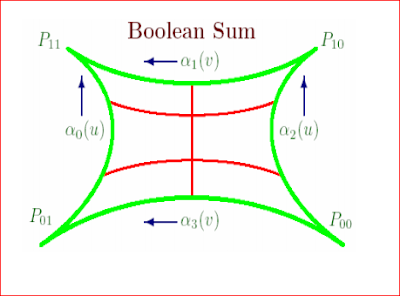
Hình vẽ: Mô hình mặt cong Boolean Sum
S(u, v) = S1(u, v) + S2(u, v) - P(u,v)
Với:
P(u,v) = (1-u)(1-v)P00 + (1-u)vP01 + u(1-v)P10 + uvP11
S1(u,v) = va0(u) + (1-v)a2(u)
S2(u,v) = ua1(v) + (1-u)a3(v);
P là các đỉnh của mảnh 4
ai(u) là các phương trình đường biên
Ví dụ về mặt Boolean Sum:
Với u = 0
S(0,v) = S1(0,v) + S2(0,v) - P(0, v)
= v a0(0) + (1 - v)a2(0) + 0a1(v)+ 1 a3(v) - (1 - v)P00 - v P01
Mặt được xây dựng trên 4 điểm và các đường cong biên, S(u,v) mặt nội suy trên 4 đường
biên.
S(u, v) = S1(u, v) + S2(u, v) - P(u,v)
Với:
P(u,v) = (1-u)(1-v)P00 + (1-u)vP01 + u(1-v)P10 + uvP11
S1(u,v) = va0(u) + (1-v)a2(u)
S2(u,v) = ua1(v) + (1-u)a3(v);
P là các đỉnh của mảnh 4
ai(u) là các phương trình đường biên
Ví dụ về mặt Boolean Sum:
Với u = 0
S(0,v) = S1(0,v) + S2(0,v) - P(0, v)
= v a0(0) + (1 - v)a2(0) + 0a1(v)+ 1 a3(v) - (1 - v)P00 - v P01
= v P01 + (1 - v)P00 + a3(v) -(1 - v)P00 - v P01
= a3(v)
= a3(v)
Mặt trượt (Sweept Surface )
5. Mặt trượt (Sweept Surface)
Hình vẽ: Mô hình mặt trượt
Sweep surface là mặt được tạo bởi bằng cách trượt một thực thể.
Ví dụ: một đường thẳng, đa giác, một đường cong, một hình… dọc theo một đường trong
không gian.
Q(u,v) = P(u)*[ T(v) ]
P(u) thực thể cần trượt
[ T(v) ] là ma trận biến đổi ([ T(v) ] có thể là ma trận tịnh tiến, quay, hay tỉ lệ …hoặc là kết
hợp của nhiều phép biến đổi đó).
Ví dụ:
P1[000], P2[03 0]
P(t) = P1 + (P2 – P1) *u = [0 3u01]
0 ≤u,v≤ 1
Ví dụ về mặt trượt (Sweept Extrusion)
Hình vẽ: Mô hình mặt trượt
Sweep surface là mặt được tạo bởi bằng cách trượt một thực thể.
Ví dụ: một đường thẳng, đa giác, một đường cong, một hình… dọc theo một đường trong
không gian.
Q(u,v) = P(u)*[ T(v) ]
P(u) thực thể cần trượt
[ T(v) ] là ma trận biến đổi ([ T(v) ] có thể là ma trận tịnh tiến, quay, hay tỉ lệ …hoặc là kết
hợp của nhiều phép biến đổi đó).
Ví dụ:
P1[000], P2[03 0]
P(t) = P1 + (P2 – P1) *u = [0 3u01]
0 ≤u,v≤ 1
Ví dụ về mặt trượt (Sweept Extrusion)
Hình vẽ: Hình thành mặt trượt
Mặt tròn xoay (Revolution surface)
6. Mặt tròn xoay (Revolution surface)
Hình vẽ: Mô hình mặt tròn xoay
Mặt được xây dựng bởi đường thẳng hay một đường cong phẳng, quanh một trục trong
không gian.
Giả sử đường cong phẳng có dạng:
P(t)=[x(t) y(t) z(t)] 0≤t≤tmax
Ví dụ: quay quanh trục x một thực thể nằm trên mặt phẳng xoy, phương trình bề mặt là
Q(t, f ) = [ x(t) y(t) cosfz(t) sinf ]
Ví dụ: Mặt tròn xoay
P1[1 1 0] và P2[6 2 0] nằm trong mặt phẳng xoy. Quay đường thẳng quanh trục ox sẽ
được một mặt nón. Xác định điểm của mặt tại t=0.5, f =p/3.
Phương trình tham số cho đoạn thẳng từ P1 tới P2 là:
Hình vẽ: Mô hình mặt tròn xoay
Mặt được xây dựng bởi đường thẳng hay một đường cong phẳng, quanh một trục trong
không gian.
Giả sử đường cong phẳng có dạng:
P(t)=[x(t) y(t) z(t)] 0≤t≤tmax
Ví dụ: quay quanh trục x một thực thể nằm trên mặt phẳng xoy, phương trình bề mặt là
Q(t, f ) = [ x(t) y(t) cosfz(t) sinf ]
Ví dụ: Mặt tròn xoay
P1[1 1 0] và P2[6 2 0] nằm trong mặt phẳng xoy. Quay đường thẳng quanh trục ox sẽ
được một mặt nón. Xác định điểm của mặt tại t=0.5, f =p/3.
Phương trình tham số cho đoạn thẳng từ P1 tới P2 là:
P(t) = [ x(t) y(t) z(t) ] = P1 + (P1 - P2)t 0 ≤t≤ 1
Với các thành phần Đề-các:
x(t) = x1 + (x2- x1)t = 1+5t
y(t) = y1 + (y2- y1)t = 1+t
z(t) = z1 + (z2- z1)t = 0
Với các thành phần Đề-các:
x(t) = x1 + (x2- x1)t = 1+5t
y(t) = y1 + (y2- y1)t = 1+t
z(t) = z1 + (z2- z1)t = 0
Đăng ký:
Nhận xét (Atom)