Mặt cong B-Spline

1. Mặt cong B-Spline

Phương trình mặt B-spline:

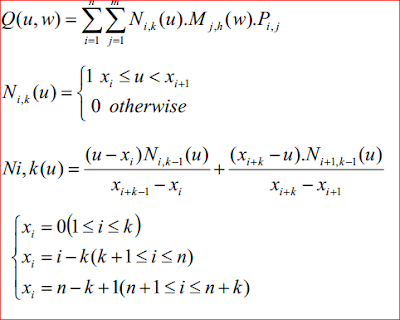
P
ij là điểm kiểm soát
N và M là đa thức B-spline
Với các mặt cong mở mặt cong phụ thuộc vào các nút vector
Đặc điểm của mặt cong B-Spline
*ƒ Số bậc caonhất của bề mặt theo mỗi hướng thì bằng số điểm kiểm soát -1 theo hướng đó.
ƒ *Đạo hàm riêng của phương trình bề mặt theo mỗi tham biến có bậc bằng số điểm kiểm
soát theo tham biến đó trừ 2.
ƒ* Bề mặt B-spline thì không chịu ảnh hưởng của phép biến đổi anfine. Bề mặt sẽ thay đổi
nếu ta thay đổi đa giác kiểm soát.
ƒ *Ảnh hưởng của một điểm kiểm soát đơn được giới hạn bởi + - k/2 h/2 khoảng đối với mỗi
tham số.
ƒ *Nếu số đỉnh của đa giác kiểm soát bằng số bậc theo mỗi tham biến và không có điểm kép
nào thì mặt B-spline sẽ chuyển thành mặt Bezier.
ƒ* Nếu các đa giác kiểm soát có dạng tam giác thì lưới đa giác kiểm soát sẽ có hình dáng gần
giống với bề mặt cong.
ƒ* Mỗi mặt B-Spline luôn nằm trong bao lồi của đa giác kiểm soát .
ƒ* Mỗi mặt B-Spline có dáng điệu luôn bám theo hình dáng của đa giác kiểm soát.

Tóm tắt:
Việc tạo ra các đường cong theo ý muốn cũng là vấn đề thường gặp khi làm việc với đồ hoạ
máy tính. Chúng ta khảo sát cách tiếp cận vẽ đường cong bằng Hermite, Bezier và B-spline. Các
cách tiếp cận này dựa trên cơ sở vẽ đường cong bằng một tập điểm mô tả hình dáng của đường
cong gọi là tập điểm kiểm soát. Khi thay đổi tập điểm này, hình dáng của đường cong sẽ thay đổi
theo. Cách tiếp cận này cho thấy sự thuận lợi và linh hoạt khi cần phải vẽ các đường cong phức
tạp và do đó nó được dùng nhiều trong thiết kế.
Một nhược điểm trong cách vẽ đường cong bằng Bezier là khi một phần của đường cong đã
đạt yêu cầu, nhưng khi hiệu chỉnh phần còn lại sẽ mất đi phần đã đạt yêu cầu, hay việc nối trơncác đường cong sẵn có. Để khắc phục các vấn đề này ta có cách tiếp cận cải tiến vẽ đường cong
bằng B-spline.
Tương tự như vậy việc biểu diễn các mặt cong trong đồ hoạ máy tính cũng là một vấn đề
cần thiết để mô tả đối tượng trong thế giới thực. Chúng ta khảo sát về các phương pháp biểu diễn
mặt cong thông qua phương trình tham số. Trong đó, phương trình tham số của một mặt có dạng
là một phương trình tham số hai biến p(u,v) và một điểm bất kỳ trên mặt sẽ được biểu diễn dưới
dạng p(u,v)= (x(u,v), y(u,v), z(u,v)). Chúng ta khảo sát một số mặt đơn giản như: mặt kẻ, mặt tròn
xoay, mặt trượt và mặt Boolean Sum.
Trên cơ sở các đường cong bằng Hermite, Bezier và B-spline chúng ta cũng xây dựng được
các mặt Hermite, Bezier và B-spline.